Kani’s Method | Advantages of Kani’s Method | How to Use Kani’s Method for Analysis | Procedure of Kani’s Method
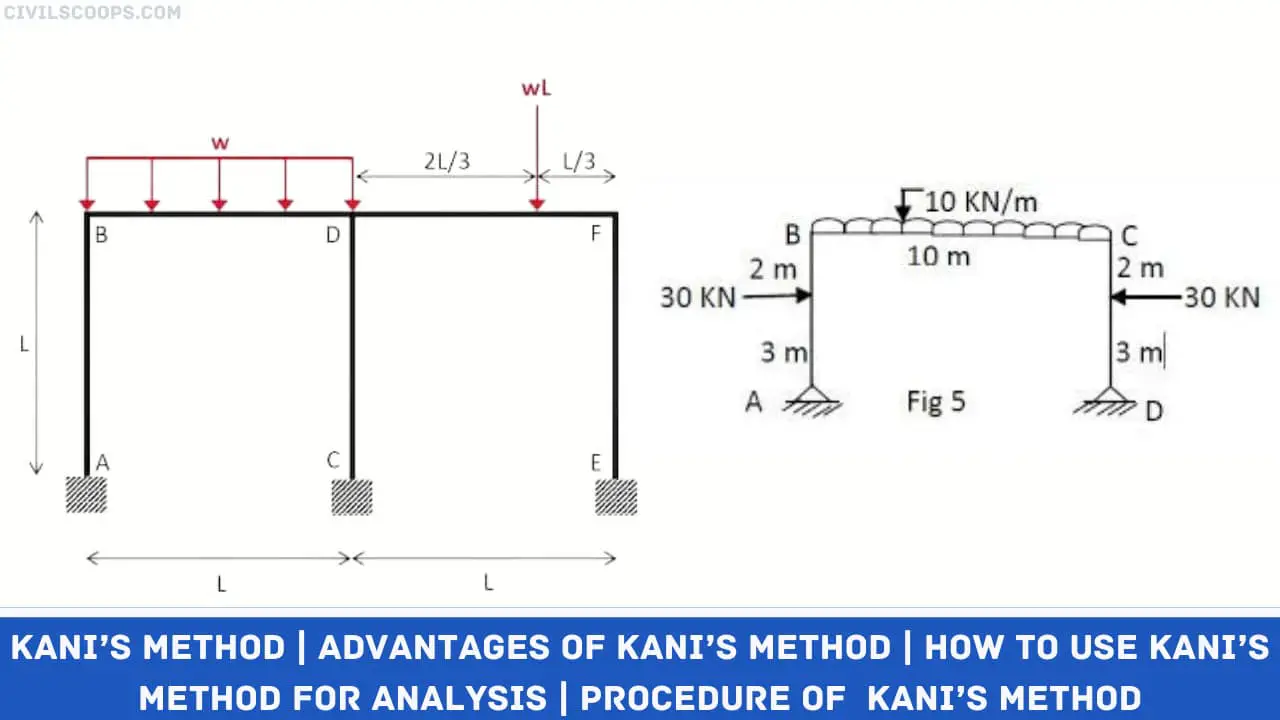
Table of Contents
Kani’s Method
Structural analysis is one of the most important parts of civil engineering. The construction of high rise buildings and multi-storey buildings are increasing day by day.
The high rise building requires the perfect analysis of frames and different structure of members features has a number of joints. Kani’s method was developed by Gasper Kani in the year 1940. The Kani’s method consists of the distribution of the unknown fixed end moments of the different structural members to the adjacent joints in order to satisfy the conditions of continuity of slopes and displacements.
In this article,you will get to know about the Kani’s method and the Advantages of Kani’s method and how to use kani’s method. Kani’s method is also known as the Rotation contribution method. It is a developed method of iteration for the statically
indeterminate buildings and structures which is an approximate method that can save a great deal of time compared to the moment distribution method. Kani’s method is considered for the further simplification of the moment distribution method for solving various problems.
This method consists of allotting the an identified within moments of the various structural members to the adjoining joints. Kani’s method involves the distribution of the unknown fixed end moments of the different structural members to the adjacent
joints in order to satisfy the different conditions of continuity of slopes and displacements.
Advantages of Kani’s Method
Here, the pros of Kani’s Method are as follows.
- There are various advantages of this method in structural analysis of members are as follows
- The main advantage of using Kani’s method for structural analysis is because it is self-corrective.
- The Hardy cross method distributed only the unbalanced moments at the joints, and the Kani’s method distributes the total joints
moment at any stage. - Kani’s method is simple and easy as compared to other methods.
- All the computations of this method are carried out in a single line diagram of the structure.
- The effects of joint rotations are considered in each cycle of iteration.
- The convergence in this method is very fast which leads to the solution in just a few cycles of iterations.
How to Use Kani’s Method for Analysis?
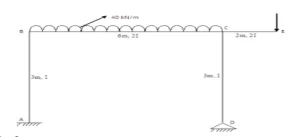
The junction of the beam with the column consists of rigid joints.
- For all beams, I => 2I
- For all columns, I => I
Framed structures are rarely symmetric and subjected to side sway that’s why the Kani’s method is best and much simpler as compared to the other types of methods.
Procedure of Kani’s Method
Step 1
- Rotation stiffness at every end of the members of a structure is determined depending upon the various end conditions.
- When the Both ends are fixed
Kij= Kji= EI/L
- When the near ends are fixed and the far ends are simply supported
Kij= ¾ EI/L; Kji= 0
Step 2
- Rotational factors which are computed for all the members at each joint it is given are as follows
Uij= -0.5 (Kij/ ?Kji)
- The sum of the rotational factors at the joint is -0.5. The Fixed end moments including transitional moments and the moment releases and carry over moments are computed for the various members.
- The sum of the FEM at a joint is entered in the central square drawn at the various joints.
Step 3
- Iterations can be commenced at any joint and the iterations commence from the left end of the structure
- It is generally given by the following equations
M?ij = Uij [(Mfi + M??i) + ? M? ji)]
Step 4
- Initially the rotational components (which is the sum of the rotational moments at the far ends of the joint) is assumed to be zero.
- The further various iterations are taken into account of the rotational moments of the previous joints.
Step 5
- Rotational moments are computed at each joint successively till all the joints are processed. This process
- completes one cycle of iteration.
Step 6
- The above steps 4 and 5 are repeated till the difference in the values of rotation moments will form the successive cycles is neglected.
Step 7
- Final moments in the various members at each joint are calculated from the rotational members of the final iterations.
Mij = (Mfij + M??ij) + 2 M?ij + M?jii
Step 8
- Displacement factors are calculated for each storey given by
Uij = -1.5 (Kij/?Kij)
[su_box title=”FAQ” style=”default” box_color=”#333333″ title_color=”#FFFFFF” radius=”3″ class=”” id=””]
Kani’s Method
Kani’s method was introduced by Gasper Kani in 1940’s. It involves distributing the unknown fixed end moments of structural members to adjacent joints, in order to satisfy the conditions of continuity of slopes and displacements. Kani’s method is also known as Rotation contribution method.
Advantages of Kani’s Method
- All the computations are carried out in a single line diagram of the structure.
- The effects of joint rotations and sway are considered in each cycle of iteration. Henceforth, no need to derive and solve the simultaneous equations.
Kani’s Method for Continuous Beams
The method provides a iterative scheme for employing slope deflection method. It is mostly recognized for frame analysis. It comprises allotting the unidentified fixed end moments of structural members to adjoining joints, with the purpose of meeting the conditions of continuity of slopes and displacements.
[/su_box]
[su_note note_color=”#F2F2F2 ” text_color=”#333333″ radius=”3″ class=”” id=””]
Like this post? Share it with your friends!
- Suggested Read –
- Material Required for Construction of WBM Road
- What Is Weep Holes | Function of Weep Holes | Types of Weep Holes
- What Is ACP | Applications of ACP Sheet | Advantage of ACP Sheet | Disadvantages of ACP Sheet
- What Is Dampness | Causes of Dampness | Effects of Dampness | Damp Proofing Materials | Methods of Damp Proofing
- What Is AAC Block | When AAC Was First Developed | Advantages of Using AAC Blocks | Disadvantage of AAC Blocks | Properties of AAC Blocks
[/su_note]
Originally posted 2022-07-15 14:50:28.
